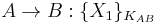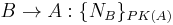Security protocol notation

In cryptography, security (engineering) protocol notation is a way of expressing a protocol of correspondence between entities of a dynamic system, such as a computer network. In the context of a formal model, it allows reasoning about the properties of such a system.

The standard notation consists of a set of individuals (traditionally named Alice, Bob, Charlie, and so on) who wish to communicate. They may have access to a server S, shared keys K, timestamps T, and can generate nonces N for authentication purposes.

A simple example might be the following:

A\rightarrow B:\{X_1\}_{K_{AB}}

This states that Alice intends a message for Bob consisting of a plaintext 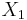X_1 encrypted under shared key KAB.

Another example might be the following:

B\rightarrow A:\{N_B\}_{PK(A)}

This states that Bob intends a message for Alice consisting of a nonce encrypted using public key of Alice.

A key with two subscripts is a symmetric key shared by the two corresponding individuals. A key with one subscript is the public key of the corresponding individual. A private key is represented as the inverse of the public key.

The notation specifies only the operation and not its semantics — for instance, private key encryption and signature are represented identically.

We can express more complicated protocols in such a fashion. See Kerberos as an example. Some sources refer to this notation as Kerberos Notation.[1] Some authors consider the notation used by Steiner, Neuman, & Schiller[2] as a notable reference. [3]

Several models exist to reason about security protocols in this way, one of which is BAN logic.

References

  1. ^ Chappell, David (1999). "Exploring Kerberos, the Protocol for Distributed Security in Windows 2000". Microsoft Systems Journal. http://www.microsoft.com/msj/0899/kerberos/kerberos.aspx. 
  2. ^ Steiner, J. G.; Neuman, B. C.; Schiller, J. I. (February 1988). "Kerberos: An Authentication Service for Open Network Systems" (PDF). Proceedings of the Winter 1988 Usenix Conference. Usenix. Berkeley, CA: USENIX Association. pp. 191–201. http://clifford.neuman.name/publications/1988/198802-Usenix-Kerberos/198802-Usenix-Steiner-Neuman-Schiller-Kerberos.pdf. Retrieved 2009-06-10. 
  3. ^ Davis, Don; Swick, Ralph (1989-03-17) (PS). Workstation Services and Kerberos Authentication at Project Athena. p. 1. ftp://athena-dist.mit.edu/pub/ATHENA/kerberos/doc/user2user.ps. Retrieved 2009-06-10. "…our notation follows Steiner, Neuman, & Schiller,…"